Processing 入門

17．ブロック崩し４ ブロックとの当たり判定

今回は「ブロック崩し３ 自機との当たり判定」の続きです。

プログラミングでよく使う計算式は、ほとんどが中学レベルのものです。
ゲームによっては三角関数など高校レベルのときもあります。
今回は中学レベルです。しかし、演算の優先は知っている必要がありますね。
ただ、これもカッコ（ ）を使えば簡単になります。
カッコの中を優先的に計算する決まりがあるからです。

ブロックを並べて表示しよう

それでは、ブロックを並べて表示してみましょう。
前回の「みどりを救えゲーム」でも使った ％（割った余りを算出）を活用します。

実行すると次のように表示されます。
見た目はもうブロック崩しです。

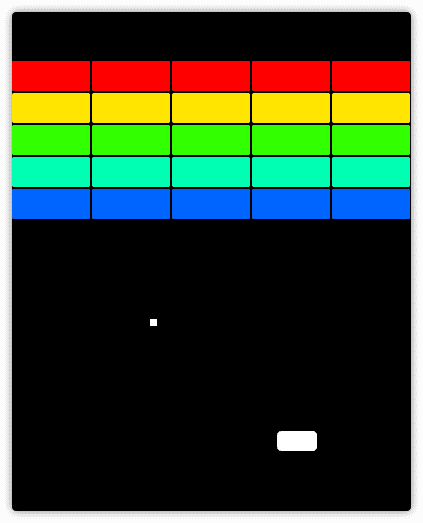
並べるときによく使う計算式を使っています。（89、90行目）
このような式を初めて見たとき、理解できないときがありますよね。
そんなときは for 文の回数を減らして実行してみましょう。
次の例では４回だけにしました。
これで変数 i の値がどのように影響するか、イメージし易くなったと思います。

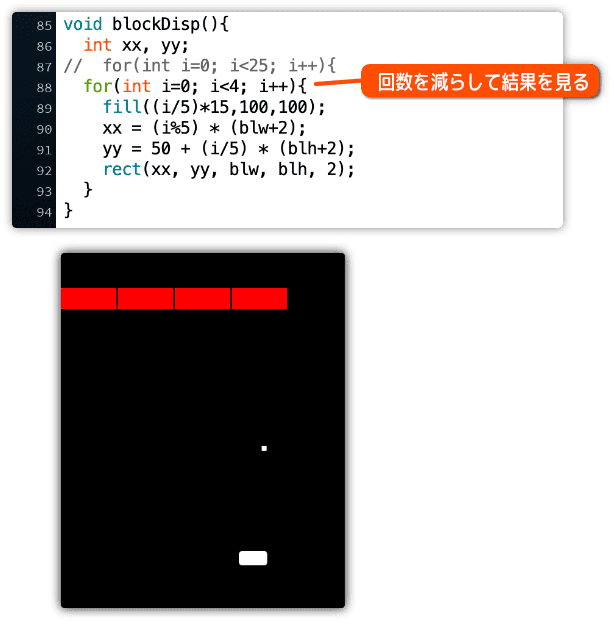
なお、ブロックの高さ（ blh ）と幅（ blw ）に＋２しているのは、
ブロックの間にすき間を作るためです。

玉とブロックの当たり判定をしよう

ここでビックリマークのキーを覚えましょう。
エクスクラメーションマークとも言います。
次のところにあります。シフトキーを押しながら入力します。

これから当たり判定をして、ブロックを消すところまで行います。
配列変数 blf をブロックと同じ数だけ用意します。
この変数が 0 のときは表示させず、1 のときは表示するように使います。

ブロックの表示で、表示と非表示を切り替えるようにします。
ついでに当たり判定も組み込みます。（96行目）

当たり判定の中で 105行目は注意です。
否定を使っています。
つまり、当たり判定の式が成立していれば 109行目に行きます。

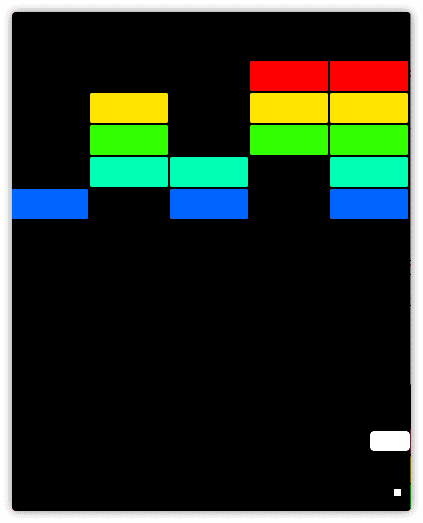
実行してみましょう。
玉と当たったブロックが次々と消えていきます。

玉を跳ね返らせよう

玉がブロックと当たったとき、跳ね返るようにします。
跳ね返りの処理と言えば、自機のときにも作りました。
しかし自機の場合は、玉が画面の上から移動してくるだけです。
それに対し、ブロックの場合は上下左右のどの方向にも対応しなければなりません。

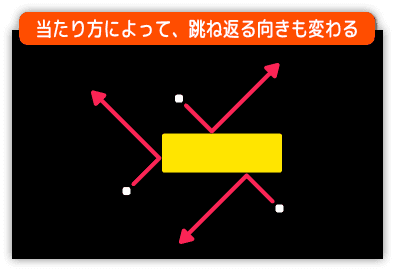
どの方向から玉が飛んできたのかチェックするため
移動前の位置を覚えておく変数を作ります。
変数 lastx と lasty を使い、移動する前の座標を退避します。（73、74行目）

跳ね返りの処理をシンプルにするため、３つのパターンのみで対応します。
移動前の玉がどの位置にいたかで分けてます。

・ブロックの幅の中にいた場合
・ブロックの高さの中にいた場合
・それ以外の場合

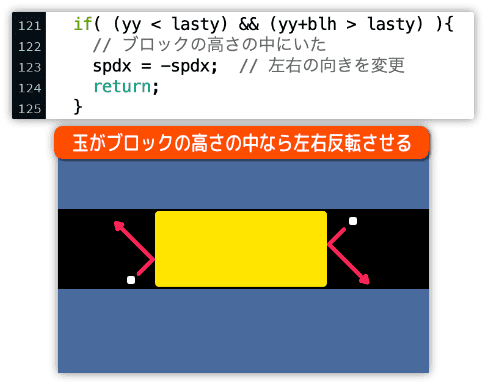
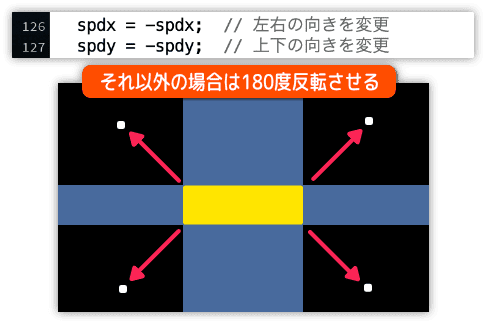
これは本当にシンプルさを優先させたプログラムです。
じっくり見ると違和感があるかもしれません。
いつか余裕がでたら、もっと複雑な当たり判定にチャレンジしてみてください。