TIPS ゲーム制作のコツ

◇ ２点間の距離による当たり判定 ◇

２つの座標の距離を算出して、当たり判定をする方法です。
シンプルな計算で行えるためよく利用されます。

下のサンプルは、これから説明する当たり判定の仕組みを使っています。

オレンジの円をマウスで操作して
ミドリの円に重ねたり、離したりしてみてください。

三平方の定理を使おう

三平方の定理とは、直角三角形の３辺の長さの関係を公式にしたものです。

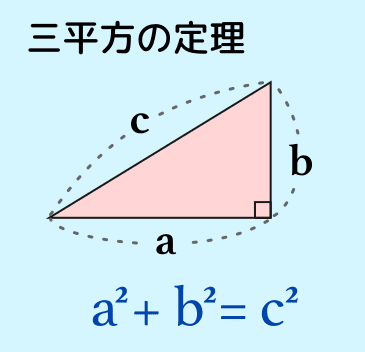
２つの円の重なり（当たり判定）を調べるには、２点の距離が必要です。
その距離を算出するために三平方の定理を使います。

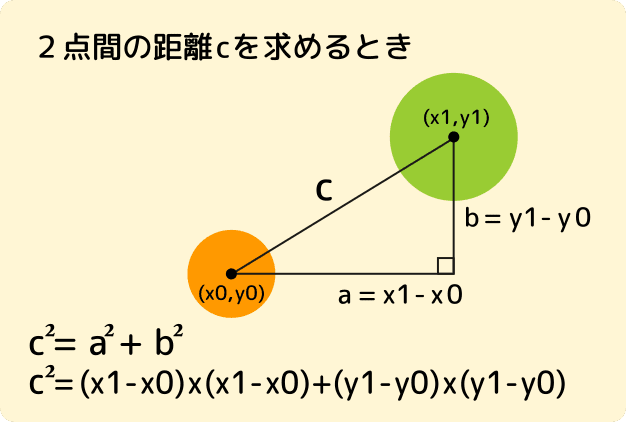
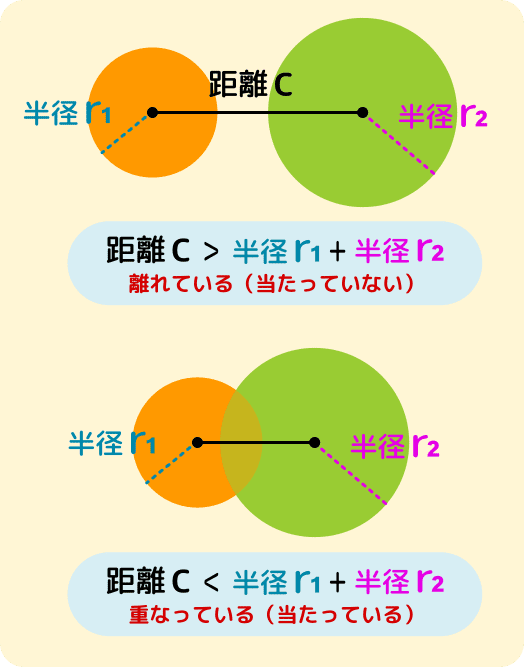
距離が分かれば円の半径から、重なり（当たり）を判定できます。

当たり判定をしているプログラムを見てみましょう。
（ページの上部で動かしていたプログラムです）

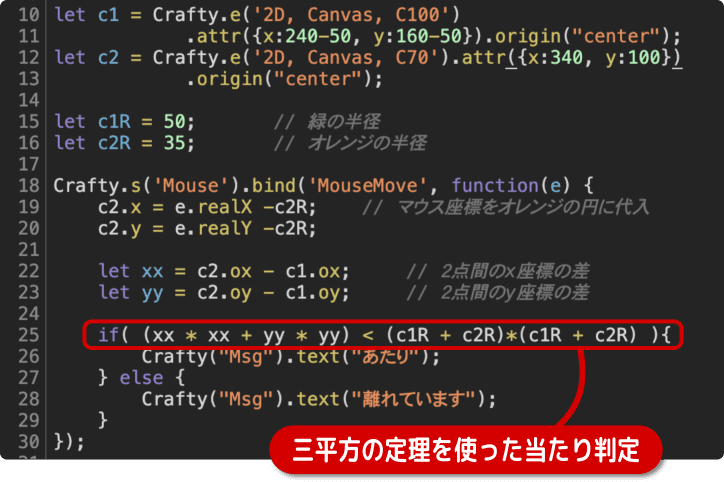
c1 は中心にあったミドリの円です。
c2 はマウスカーソルで操作できたオレンジの円です。

25行目で三平方の定理を使った当たり判定をしています。

２点間の距離を平方根で算出せず、半径側を二乗している点がポイントです。
なんども処理するようなときには、計算をできるだけ単純化させます。

２点間の距離による当たり判定の使いどころ

円と円の当たり判定には最適です。
ビリヤードゲームなどの球と球の当たりに使用します。

また、円と点(片方に厚みがない)などにも適しています。
対象物が完全な円でなくても、ゲームとしての面白さを損なわないなら使っていいと思います。

それから、当たり判定だけでなく射程を測るのにも使えます。
射程内に入った敵を自動で攻撃したいときなどの処理にいいですね。

処理の重さを考えよう

２点間の距離による当たり判定の処理は、 シンプルな四角形(矩形)同士の当たり判定より少し重いです。

当たり判定を行う対象が非常に多いならば、 まず四角形(矩形)同士の当たり判定を行ったほうがいいでしょう。

それが当たっていた時のみ、２点間の距離による当たり判定をして正確な結果を求めます。

つまり、処理の軽い判定で「当たっている可能性」を調べ、より正確な判定方法で「当たり外れ」を調べます。